逻辑回归
(1) 概述
- 逻辑回归算法用于分类问题,例如区分肿瘤的良性和恶性。空气质量的优,良,轻度污染,中度污染,重度污染等
- 预测的变量类型为离散型的变量。
- 将因变量可能属于的两个类称为负向类和正向类,因变量
y
∈
(
0
,
1
)
y\in(0,1)
y∈(0,1),其中0表示负向类(表示我们要寻找的东西不存在),1表示正向类(表示我们要寻找的东西存在)。

(2)逻辑回归模型的模型假设
- 模型: h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx)
-
g
(
x
)
g(x)
g(x)的形式为
g
(
x
)
=
1
1
+
e
−
x
g(x)=\dfrac{1}{1 +e^{-x}}
g(x)=1+e−x1,称为Sigmoid function。

- 做这个变换的目的在于,在一一映射的前提下,把函数值卡在范围 [ 0 , 1 ] [0,1] [0,1]之间,判断时就可以当 h θ ( x ) ≥ 0.5 h_\theta(x)\geq0.5 hθ(x)≥0.5时判断 y = 1 y=1 y=1,在 h θ ( x ) < 0.5 h_\theta(x){<}0.5 hθ(x)<0.5 时判断 y = 0 y=0 y=0,而 x = 0 x=0 x=0时 h θ ( x ) h_\theta(x) hθ(x)恰好为 0.5 0.5 0.5,因此当 x > 0 x>0 x>0时取 1 1 1,当$ x{<} 0$时取 0 0 0。
- h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta(x)=P(y=1|x;\theta) hθ(x)=P(y=1∣x;θ)即 h θ ( x ) h_\theta(x) hθ(x)是一个概率值,是在 x ; θ x;\theta x;θ的前提下。
(3)判定边界
- 所谓的判定边界其实就是画出的一条线,在线的不同侧是不同的类。
- 线性边界

在这里 h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2) hθ(x)=g(θ0+θ1x1+θ2x2)而 θ \theta θ是向量[3,-1,-1],其实也就是 x 1 + x 2 ≥ 3 x_1+x_2\geq3 x1+x2≥3,即用直线 x 1 + x 2 = 3 x_1+x_2=3 x1+x2=3将这两块区域分开。(有点类似线性规划)。 - 圆形边界

h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 ) h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2) hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22)求解可知 [ θ 0 , θ 1 , θ 2 , θ 3 , θ 4 ] = [ − 1 , 0 , 0 , 1 , 1 ] [\theta_0,\theta_1,\theta_2,\theta_3,\theta_4]=[-1,0,0,1,1] [θ0,θ1,θ2,θ3,θ4]=[−1,0,0,1,1]。相当于 x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1是那条分界线。
(4)代价函数 - 变量说明
- 训练集: { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) … ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)})\dots(x^{(m)},y^{(m)})\} {(x(1),y(1)),(x(2),y(2))…(x(m),y(m))}
- x ( i ) = ( x 0 , x 1 , x 2 , … , x n ) T x^{(i)}=(x_0,x_1,x_2,\dots,x_{n})^T x(i)=(x0,x1,x2,…,xn)T每一个训练元素均有n个特征值。
- y ∈ ( 0 , 1 ) , y y\in(0,1),y y∈(0,1),y取0,1中的某一个值,表示不存在或者存在。
- h θ ( x ) = 1 1 + e − θ T x h_\theta(x)=\dfrac{1}{1+e^{-\theta^{T}x}} hθ(x)=1+e−θTx1
- 函数规定
-
如果继续沿用之前的定义,令代价函数 J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\dfrac{1}{m}\sum\limits_{i=1}\limits^{m}\dfrac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=m1i=1∑m21(hθ(x(i))−y(i))2。这里会产生一个问题,即 J ( θ ) J(\theta) J(θ)这个函数不再是一个凹函数了,因此不能很好地使用梯度下降法求得全局的最小值。
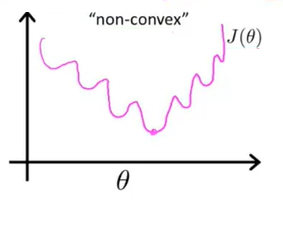
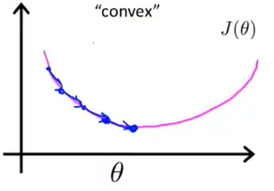
-
为保证函数还是一个凹函数,引入下面的代价函数:
⭐️ c o s t ( h θ ( x ) , y ) = { − log ( h θ ( x ) ) , i f y = 1 − l o g ( 1 − h θ ( x ) ) , i f y = 0 cost(h_\theta(x),y)=\begin{cases} -\log(h_\theta(x)), & if{\quad}y=1\\ -log(1-h_\theta(x)), & if{\quad}y=0 \end{cases} cost(hθ(x),y)={−log(hθ(x)),−log(1−hθ(x)),ify=1ify=0
1️⃣ 当 y = 1 y=1 y=1时,函数图像是:

可以看出,随着 h θ ( x ) h_\theta(x) hθ(x)的值越来越接近1,代价函数的值趋向0,这是符合 y = 1 y=1 y=1的这个前提的。
2️⃣当 y = 0 y=0 y=0时,函数图像是:

可以看出,随着 h θ ( x ) h_\theta(x) hθ(x)的值越来越接近1,代价函数的值趋向无穷,这是符合 y = 0 y=0 y=0的这个前提的。
综合上两种情况
c o s t ( h θ ( x ) , y ) = − y log ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) cost(h_\theta(x),y)=-y\log(h_\theta(x))-(1-y)log(1-h_\theta(x)) cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
代入后得到:
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=\dfrac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))] 即: J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=-\dfrac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。算法为:Repeat { θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j - \alpha \dfrac{\partial}{\partial\theta_j} J(\theta) θj:=θj−α∂θj∂J(θ) (simultaneously update all ) }
求导后得到:
Repeat { θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) \theta_j := \theta_j - \alpha \dfrac{1}{m}\sum\limits_{i=1}^{m}{{\left( {h_\theta}\left( \mathop{x}^{\left( i \right)} \right)-\mathop{y}^{\left( i \right)} \right)}}\mathop{x}_{j}^{(i)}) θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)) (simultaneously update all ) }(这个求导后的式子可以推出来,但这里略去证明)
-
(5)高级优化
- 共轭梯度法 BFGS (变尺度法) 和L-BFGS (限制变尺度法)
- 函数测试:
function [jVal, gradient]=costFunction(theta) jVal=(theta(1)-5)^2+(theta(2)-5)^2; gradient=zeros(2,1); gradient(1)=2*(theta(1)-5); gradient(2)=2*(theta(2)-5); endoptions=optimset('GradObj','on','MaxIter',100); initialTheta=zeros(2,1); [optTheta, functionVal, exitFlag]=fminunc(@costFunction, initialTheta, options);
(6)多类别分类
- 思想:转化为二分类问题。
- 构造:
\quad 对 y ∈ { 1 , 2 , … , n } y\in\{1,2,\dots,n\} y∈{1,2,…,n}的类别进行分划,将 y = i y=i y=i标记为正向类,把其余的标记为负向类,完成这样的一个标记可以求出一个分划函数 h θ ( x ) h_\theta(x) hθ(x)其中对每一个 i i i取 h θ ( i ) ( x ) = p ( y = i ∣ x ; θ ) h^{(i)}_\theta(x)=p(y=i|x;\theta) hθ(i)(x)=p(y=i∣x;θ)。 - 预测:
\quad 输入一个 x x x,找到 max i h θ ( i ) ( x ) \max\limits_{i}h^{(i)}_\theta(x) imaxhθ(i)(x),即让 y = i y=i y=i的概率最大,这时,明显 y y y应当取 i i i。 - 例如对三类的情况:

(7)作业题目(matlab)
- sigmoid函数计算
function g = sigmoid(z) g = zeros(size(z)); g=1./(1+exp(-z)); end - 代价函数的计算(带有正则化项)
function [J, grad] = costFunctionReg(theta, X, y, lambda) m = length(y); % number of training examples J = 0; grad = zeros(size(theta)); h_theta=sigmoid(X*theta); theta(1,1)=0;%这里将J(1,1)置为0目的是不对theta0进行优化 J=(1/m)*(-1.0*y'*log(h_theta)-(1-y)'*log(1-h_theta))+(lambda/(2*m))*(theta'*theta); grad=(1/m)*X'*(h_theta-y)+(lambda/m)*theta; end - 进行特征映射
function out = mapFeature(X1, X2) % MAPFEATURE Feature mapping function to polynomial features % % MAPFEATURE(X1, X2) maps the two input features % to quadratic features used in the regularization exercise. % % Returns a new feature array with more features, comprising of % X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc.. % % Inputs X1, X2 must be the same size % degree = 6; out = ones(size(X1(:,1))); for i = 1:degree for j = 0:i out(:, end+1) = (X1.^(i-j)).*(X2.^j);%这里end+1相当于一个动态数组 end end end




![[PHP] 编译构建最新版PHP源码](https://images2017.cnblogs.com/blog/726254/201801/726254-20180113194738801-448675742.jpg)

